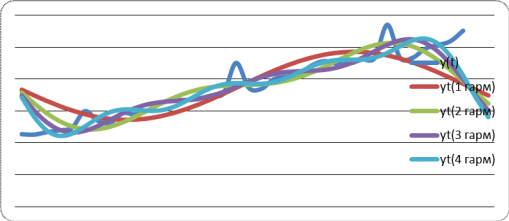
Метод Шискина-Эйзенпресса

На рисунке изображены графики, построенные по исходному ряду данных, а также по рядам с 1-ой, 2-мя, 3-мя и 4-мя гармониками.

Далее необходимо определить, какой из данных рядов наилучший, используя отклонения фактических значений от расчетных, дисперсии и коэффициенты детерминации:

Таблица 2

Из таблицы 2 делаем вывод, что наилучшим образом отражает исходный временной ряд с 4-мя гармониками, потому что его отклонение фактических значений от расчетных наименьшее, а коэффициент детерминации самый высокий.[3]

Чаще всего в экономике встречаются временные ряды, имеющие тенденцию, а значит такие ряды не являются стационарными.

В этом случае, чтобы применить ряд Фурье, необходимо привесит его к стационарному виду.

Для этого находится линейный тренд

и применяется ряд Фурье для остаточных величин

.

Существует также и другой подход.

Для ряда Фурье используются первые разности:

Это равносильно учету линейного тренда.

Если временной ряд обладает линейным трендом и периодическими колебаниями, то строится суммарный прогноз, то есть прогноз по тренду плюс прогноз по ряду Фурье для остаточных величин.

Таким образом, ряд Фурье используется для отображения и прогнозирования динамики показателей с сезонными колебаниями.[5]