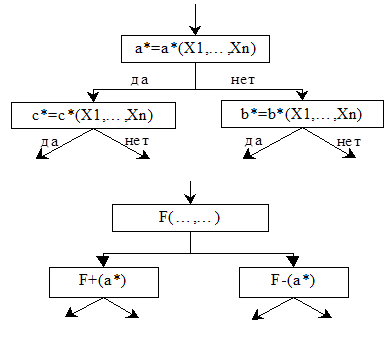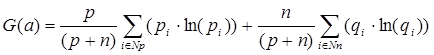Реализация алгоритмов индуктивного вывода
Информационная мера Работа алгоритма индуктивного вывода основана на использовании информационной меры (см. рис.8). Она представляет собой функционал, который на каждом шаге построения решающего правила производит оценку информативности (полезности) имеющихся элементарных свойств. Для конкретного свойства а функционал G (а) , который и называется информационной мерой, рассчитывается следующим образом:
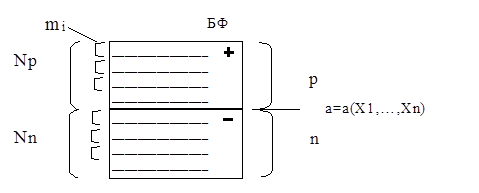
где а - элементарное свойство, т.е. логическая функция от показателей и параметров; p - число примеров в базе фактов, на которых свойство а принимает значение «истинно»; n - число примеров в базе фактов, на которых свойство а принимает значение «ложно»; Np- число групп различных значений заключений Y для той части базы фактов, на которой свойство а принимает значение «истинно»; Nn- число групп различных значений заключений Y для той части базы фактов, на которой свойство а принимает значение «ложно»; pi=mi/p, где mi - число примеров, принадлежащих к i-й группе, находящейся в той части базы фактов, где свойство а принимает значение «истинно»; qi=mi/n, где mi - число примеров, принадлежащих к i-й группе, находящейся в той части базы фактов, где свойство а принимает значение «ложно». Рисунок 8. Расчет информационной меры
Множество элементарных свойств При формировании решающего правила алгоритм индуктивного вывода использует специальное множество - множество элементарных свойств, обозначим его через А. Множество А образуют элементарные предикаты - логические функции от показателей и параметров простейшего вида. Они являются основой для построения более сложных. С практической стороны множество элементарных свойств - это множество простейших реально существующих свойств экономического объекта или явления, которые образуют более сложные, содержательные. Использование в качестве множества А элементарных свойств типа "сравнение показателя с пороговым значением" образует семейство сравнений следующего вида: Xi<rik где Xi - величина показателя или параметра; rik - величина порогового значения. В качестве элементарных свойств могут быть рассмотрены предикаты типа "сравнение значений показателей между собой": Xi<Xj , где Xi ,Xj - значения показателей или параметров. Дальнейшее расширение множества А может состоять в сравнении арифметических выражений показателей и параметров между собой и с пороговыми значениями. На самом деле, в качестве множества А может быть использовано любое количество логических функций на показателях и параметрах. Характер множества элементарных свойств определяет многообразие решающих правил, а, соответственно, и многообразие содержательных свойств экономического объекта или явления, которые определяются (регистрируются) решающим правилом. Пример Оно может состоять из следующих подмножеств; А = А1ÈА2ÈА3ÈА4 , где А1 - сравнение параметров с пороговыми значениями; |