Некоторые сведения из теории вероятности, использованные для решения задачи парковки

Пусть фиксированная неотрицательная целочисленная функция от, определенная при и удовлетворяющая условию и .

Рассмотрим первые машин, находящихся на отрезке . Обозначим через расстояние между 0 и самой левой машиной;

- расстояние между этой машиной и машиной, стоящей второй слева и так далее.

- расстояние между машиной, находящейся на правом краю и . Тогда условное распределени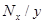е , где 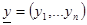такое же, как распределение при независимых. Следовательно, условное

распределение 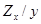равно распределению 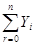, где - независимое и определено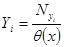

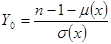
По лемме 1, где получаем 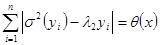или

(2.2.18) для каждого .

Отсюда следует для условных дисперсии .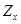

Таким образом верно для 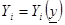для всех достаточно больших и всех случайных . Из условия следует .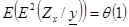

Пусть - событие: такое, что 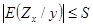, тогда из условия следует, что 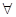фиксированного выполняется и при 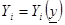удовлетворяет условию .

Определим функцию , положив 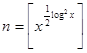и обозначим событие: 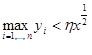. Возьмем и разделим отрезок на 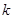интервалов одинаковой длины, обозначенных 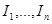, тогда, если условие 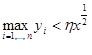неверно, принимается, что, по крайней мере, один из интервалов 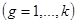разбивается по первым припаркованным на стоянку машинам.

Вероятность, это меньше, чем и , при [5]. Следовательно, .