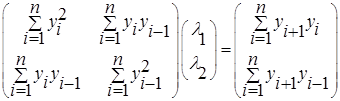Оценивание параметра авторегрессии методом МНК
Для получения оценки МНК параметра  для модели авторегрессии 1-го порядка рассмотрим сумму квадратов отклонений наблюдаемых значений переменной
для модели авторегрессии 1-го порядка рассмотрим сумму квадратов отклонений наблюдаемых значений переменной  от ожидаемых значений
от ожидаемых значений

Необходимое условие минимума  приводит к следующей оценке
приводит к следующей оценке
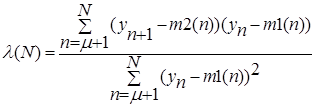 (5)
(5)
Для модели 2-го порядка сумма квадратов отклонений наблюдаемых значений от ожидаемых значений имеет вид

Необходимое условие минимума 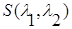 приводит к следующей системе уравнений
приводит к следующей системе уравнений
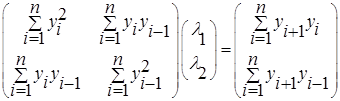
2.2 Фильтр Калмана
Фильтр Калмана также можно использовать для оценки параметра модели.
Рассматривается система линейных разностных уравнений вида
 ,
,  (6)
(6)
 ,
, 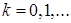 (7)
(7)
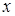 - n-мерный вектор состояний, z - l-мерный вектор измерений.
- n-мерный вектор состояний, z - l-мерный вектор измерений. 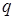 и
и 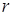 - последовательность гауссовских случайных величин с нулевым математическим ожиданием. Будем считать что они независимы между собой.
- последовательность гауссовских случайных величин с нулевым математическим ожиданием. Будем считать что они независимы между собой.
Задача состоит в том, чтобы на основе полученных измерений  получить оценку
получить оценку 
Оценка вычисляется как решение разностного уравнения
 ,
,  (8)
(8)
- матричный коэффициент,  - невязка. Чем она меньше, тем ближе оценка
- невязка. Чем она меньше, тем ближе оценка  к истинному значению. Коэффициент K выбирается таким образом, чтобы оценка
к истинному значению. Коэффициент K выбирается таким образом, чтобы оценка  была несмещённой с минимальной матрицей ковариаций.
была несмещённой с минимальной матрицей ковариаций.
Если ввести ошибку  , то эта ошибка будет удовлетворять следующему уравнению:
, то эта ошибка будет удовлетворять следующему уравнению:
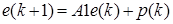 ,
,
где


 - последовательность гауссовских случайных величин со свойствами
- последовательность гауссовских случайных величин со свойствами
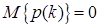

Далее введём квадратную матрицу
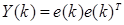

Введём  и
и 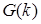 как среднее и матрицу ковариации
как среднее и матрицу ковариации 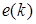
Получим следующее
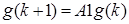

Осталось выбрать K таким образом, чтобы минимизировать 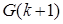
Представим правую часть в виде полного квадрата относительно K:
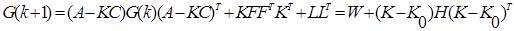
Из последнего равенства получим следующее:

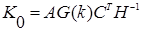 (9)
(9)
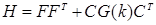 (10)
(10)
 - оптимальный коэффициент.
- оптимальный коэффициент.
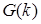 - решение уравнения Риккати. Для упрощения моделирования
- решение уравнения Риккати. Для упрощения моделирования 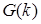 заменяем стационарным значением.
заменяем стационарным значением.  , которая находится из алгебраического уравнения Риккати
, которая находится из алгебраического уравнения Риккати



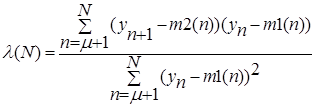 (5)
(5)