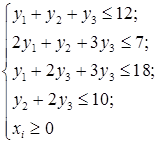Модель межотраслевого баланса

Итерация 3

Достигнуто оптимальное решение, т.к. в строке целевой функции нет положительных коэффициентов.

Оптимальное значение функции Q(x)= 326

достигается в точке с координатами:

(18; 0; 0; 11; 0; 1; 0)

Максимальная прибыль предприятия составит 326 денежных единиц, если оно выпустит 18 единиц продукции 1-го вида, 11 единиц продукции 4-го вида, а продукцию 2-го и 3-го вида выпускать не будет. При этом ресурс 2-го вида будет израсходован не полностью.

Составим модель двойственной задачи.

Напишем матрицу исходной задачи

и транспонируем её .

По теореме двойственности получим. Преобразуем ограничения - неравенства:

По теореме двойственности

Функция общая оценка сырья. Каждое ограничение системы представляет неравенство, где левая часть - оценка видов ресурсов, а правая - стоимость единицы продукции. Запишем каноническую форму математической модели двойственной задачи, введя дополнительные (балансовые переменные) , , , .

Переменные являются базисными, а - свободными. Переменные являются свободными, а - базисными. Сопоставим базисные переменные прямой задачи, свободным переменным двойственной задачи, и наоборот.

Соответствие между переменными двойственной задачи имеет вид:

.

Оптимальный план двойственной задачи имеет вид

Y=(7; 0; 5; 0; 22; 4; 0)

Экономический смысл оптимального решения двойственных задач представлен в следующей таблице.
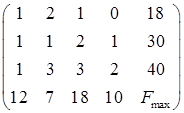