Анализ по критерию Дункана
Вычисленный выборочный коэффициент корреляции равен коэффициенту корреляции между переменными, выраженными в натуральном масштабе. Уравнение регрессии между нормированными переменными не имеет свободного члена и принимает вид:
Коэффициенты уравнения находятся из условия:
Условия минимума функции S определяются так же, как для зависимости одной переменой и система нормальных уравнений имеет вид:
Умножим левую и правую части системы уравнений на 1/(n-1). В результате при каждом коэффициенте aj получается выборочный коэффициент корреляции r*. Принимая во внимание, что:
Получаем систему нормальных уравнений в виде:
Составим систему нормальных уравнений с учетом вычисленных коэффициентов a1 + 0.526a2 - 0.945a3 = 0.488, .526a1 + a2 - 0.004a3 = 0.839, 0.945a1 + 0.004a2 + a3 = -0.025. Решая систему получим
Рассчитывают коэффициент множественной корреляции:
R = 0.838 Коэффициент множественной корреляции служит показателем силы связи для множественной регрессии: 0≤R≤1. От уравнения можно перейти к натуральному масштабу по формулам:
y = -0.117x1 + 0.901x2 - 0.139x3 Регрессионный анализ |


 (71)
(71)

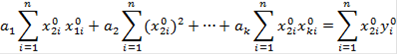 (72)
(72)

 (73)
(73)
 (64)
(64)