Общие сведения о регрессионном анализе и методе наименьших квадратов

εi = 0) и неизвестной постоянной σ2 (D

εi = σ2).

На практике рекомендуется, чтобы значение п превышало

k не

менее чем в три раза.

В модели (7)

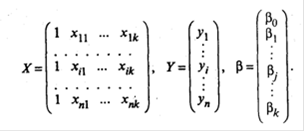
В первом столбце матрицы Х указываются единицы при наличии свободного члена в модели (6). Здесь предполагается, что существует переменная x0, которая во всех наблюдениях принимает значения, равные единице.

Основная задача регрессионного анализа заключается в нахождении по выборке объемом п оценки неизвестных коэффициентов регрессии β0, β1, …, βk модели (6) или вектора β в (7).

Так как в регрессионном анализе хj рассматриваются как неслучайные величины, a

M

εi = 0, то согласно (6) уравнение регрессии имеет вид

(8)

для

всех i = 1, 2,…, п, или в матричной форме:

(9)

где - вектор-столбец с элементами 1…, i,…, n.

Для оценки вектора-столбца β наиболее часто используют метод наименьших квадратов, согласно которому в качестве оценки принимают вектор-столбец b, который минимизирует сумму квадратов отклонений наблюдаемых значений уi от модельных значений i, т.е. квадратичную форму:

где символом «Т» обозначена транспонированная матрица.

Наблюдаемые и модельные значения результативного признака у показаны на рис. 1.

Рис. 2. Наблюдаемые и модельные значения результативного признака у

Дифференцируя, с учетом (9) и (8), квадратичную форму Q по β0, β1, …, βk и приравнивая частные производные к нулю, получим систему нормальных уравнений

решая которую получим вектор-столбец оценок b, где b = (b0, b1,…, bk)T. Согласно методу наименьших квадратов, вектор-столбец оценок коэффициентов регрессии получается по формуле

(11)

ХT - транспонированная матрица X;

(ХTХ)-1 - матрица, обратная матрице ХTХ.

Зная вектор-столбец b оценок коэффициентов регрессии, найдем оценку уравнения регрессии

(12)

или в матричном виде:

Оценка ковариационной матрицы вектора коэффициентов регрессии b определяется выражением

(13)

где

(14)

Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов регрессии, имеем

(15)

Значимость уравнения регрессии, т.е. гипотеза Н0: β = 0 (β0,= β1 = βk = 0), проверяется по F-критерию, наблюдаемое значение которого определяется по формуле

(16)

По таблице F-распределения для заданных α, v 1 = k + l, v2 = n - k - l находят Fкр.

Гипотеза H0 отклоняется с вероятностью