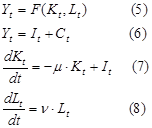Модель Солоу с непрерывным временем

Рассмотрим моменты времени, кратные , общее число моментов .

- некоторый фиксированный момент.

Соотношения (1)-(4):

- фиксированы в интервале .

Перейдем к пределу при :

Начальные условия: K(0) = K0; L(0) = L0.

- объем выбытия из каждой единицы продукции в единицу времени;

Предположим, что It - кусочно-постоянная.

Переходные процессы в модели Солоу

Пусть

X - общий валовой продукт,

Y - валовой внутренний продукт,

Y = (1-a)X - - внутренний валовой продукт;

aX - объем продукта, используемого в процессе производства;

a - коэффициент прямых затрат (объем продукта, необходимого для производства единицы данного продукта);

Y = X - aX - чистый произведенный продукт, который можно делить на инвестиции и потребление;

- норма накопления (доля продукта используемого на инвестиции);

- коэффициент выбытия основных фондов;

- коэффициент (темп) прироста трудовых ресурсов.

Система соотношений между введенными параметрами:

Или - зависимость от времени.

Переход к относительным (удельным) показателям:

- фондовооруженность (удельный капитал);

- производительность (объем произведенного продукта на одного занятого);

Предположение на функцию F(K, L):

.

В частности, если

- функция Кобба-Дугласа

- удельный объем инвестиций;

- удельное потребление.

В дальнейшем будем предполагать, что удовлетворяет условиям:

( f(k) возрастает);

( f(k) выпукла вверх);

Преобразуем

Заметим, что :

;

Подставим в (16) и поделим на L:

Обозначим :

λ = µ + ν

Тогда:

- основное уравнение для (динамическое соотношение для , k(0)=).

Начальное условие

Исследование соотношения (19):

стационарное решение уравнения (19) - постоянная функция .

Тогда

;

;

.

Если , то из (19) получим: