Решение задачи ЛП симплекс-методом
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции F(X) = x1 + x2 при следующих условиях-ограничений:
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме):
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: Решим систему уравнений относительно базисных переменных:, x4, Полагая, что свободные переменные равны 0, получим первый опорный план:= (0,0,8,3)
Переходим к основному алгоритму симплекс-метода. Итерация №0. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.
Получаем новую симплекс-таблицу:
|


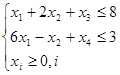 (2)
(2)