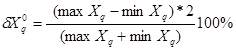Статическая оценка устойчивости чувствительности имитационной системы к изменению параметров

Каждая компонента вектора Х отклоняется от значения его в центральной точке в обе стороны на длину выбранного интервала его изменений (minXq, maxXq). Остальные компоненты вектора Х остаются без изменения и соответствуют центральной точке. При указанных значениях вектора параметров Х проводится пара модельных экспериментов и вычисляются отклики модели (minУ, maxУ), где minУ и maxУ означают соответственно векторы отклика, полученные при минимальном и максимальном значениях компоненты вектора, параметров Х. Вычисляется приращение компоненты вектора, параметров Х. Вычисляется приращение компоненты вектора модели:

Находится приращение n-й компоненты вектора отклика:

Изменение вектора У можно определять либо модулем вектора приращений, либо максимальным значением из всех n.

Результаты расчетов представлены в таблице:

dX (1/l)% =100; dY (L)% = 86

dX (t(A))% =100; dY (L)% = 181

dX (t(B))% =100; dY (L)% = 105

dX (t(B1))% =100; dY (L)% = 108

dX (t(B2))% =100; dY (L)% = 87.7

Чувствительность модели по компоненте вектора Xопределяется парой значений (). Эта пара чисел показывает, на сколько процентов может измениться отклик модели при увеличении компоненты параметра на процентов.

Можно сказать, что загрузка приборов очень чувствительна к изменению параметров входного потока, но не сильно чувствительна к изменению времени обслуживания на другом приборе, а только к изменению задержки на самом приборе.